Hola, muy buenas a todos. Llevo varios días dándole vueltas a ésto pero no consigo avanzar demasiado.
Veréis, tengo que dar una definición recursiva para el llamado "Triangulo de Pascal" que viene a ser este:
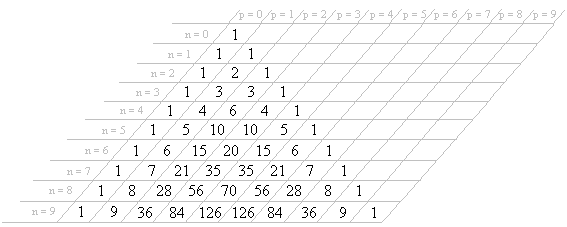
El método/función me debe calcular el número correspondiente dada una fila y columna en el nombrado triángulo. Por ejemplo para la fila(siendo n) 4 y la columna(siendo m) 1 debe de devolver 4. Aclarar, que la primera fila y columna serían 0,0. El código y la definición no hay problema, pero debo de hallar también el tamaño y complejidad del algoritmo y no consigo ver del todo el tamaño.
La definición recursiva es esta (o eso creo):

El código es este:
Integer pascal(Integer n, Integer m) {
Integer res;
if (n == m || m == 0) {
res = 1;
} else {
res = pascal(n - 1, m) + pascal(n - 1, m - 1);
}
return res;
¿Alguien sabría algo? Yo tengo varías cosas planteadas, pero es bastante laborioso de desarrollar por aquí, por eso quiero esperar a ver si alguien al menos me da una pista o alguna idea de por donde cogerlo.
Muchísimas gracias a todos de antemano.
PD: cuando digo tamaño, me refiero al tamaño del algoritmo. No creo que en este foro haga falta explicarlo XD.
 . Eres un ¡fenómeno! XD
. Eres un ¡fenómeno! XD